Hallo liebe Freude der Mikrokristalle,
in meinem letzten Blogbeitrag habe ich auf die korrekte Einstellung der Aperturblende hingewiesen.
Ich hatte beschrieben und an Hand eines Beispiels gezeigt, daß die Aperturblende nicht zu weit geschlossen werden darf, da sonst durch Beugungserscheinungen das Bildergebnis verschlechtert und sogar verfälscht wird. Auf das Phänomen der Beugung möchte ich heute etwas näher eingehen.
In der geometrischen Optik geht man davon aus, daß bei einem ideal korrigierten Objektiv, ein Objektpunkt O als Bildpunkt O‘ dargestellt wird. In der Realität sieht das aber anders aus. Statt eines Bildpunktes O‘ entsteht ein Beugungsscheibchen. Um zu demonstrieren, was es mit der Beugung auf sich hat, habe ich ein Experiment mit einem Laser Pointer durchgeführt. Dazu habe ich vor einem roten Laser Pointer eine Aluminiumfolie befestigt, in die ich ein Loch mit einem Durchmesser von ca. 0,15 mm gestochen habe. Im Abstand von ca. 3 m habe ich den Lichtfleck auf einem weißen Projektionsschirm fotografiert. Die Aufnahme wurde in einem dunklen Raum aufgenommen.

Beugungsbild eines roten Laser Pointers.
Eigentlich hätte man auf dem Projektionsschirm nur einen kleinen roten Lichtfleck erwarten sollen. Statt dessen ist ein Bild mit einem Lichtfleck in der Mitte, umgeben von abwechselnd roten und dunklen Kreisen entstanden. Es sind nicht wirklich Kreise, weil leider das Loch in der Aluminiumfolie nicht kreisrund war. Auch ist der Lichtfleck im Zentrum nicht rot, weil ich die Aufnahme absichtlich stark überbelichtet habe, um auch die umgebenden „Kreise“ besser sichtbar zu machen. Ich konnte die Kamera auch nicht mittig platzieren, da sie sonst in den Strahlengang gekommen wäre.
Wie ist dieses Bild nun zu deuten?
Es ist ganz offensichtlich, daß die aus dem kleinen Loch der Aluminiumfolie austretenden Lichtwellen sich kreisförmig auch im Schattenraum um den zentralen Lichtpunkt herum ausbreiten. Wenn sich Lichtwellen auch im Schattenraum eines Objekts ausbreiten, nennt man diese Erscheinung Beugung. Warum entstehen diese merkwürdigen roten und dunklen Ringe um das Zentrum herum? Da auch viele Schüler meinen Blog lesen, möchte ich zunächst einige grundlegende Dinge erläutern.
Der niederländische Forscher Christiaan Huygens (1629-1695) hat Gedanken zur Ausbreitung der Lichtwellen entwickelt, die noch heute gelten, und die wir das „Huygens’sche Prinzip“ nennen. Zur Darstellung der Ausbreitung von Lichtwellen verwendet man die Begriffe „Wellenfront“, „Wellennormale“ oder „Wellenstrahl“.

Wellenfronten, Wellennormale bzw. Wellenstrahl.
Die Kreise in der Skizze sind die Wellenfronten, sie stellen die maximale Auslenkung (Wellenberge) einer Welle dar. (Man denke an das Bild das entsteht, wenn man einen Stein in einen Teich mit glatter Wasseroberfläche wirft). Der Abstand λ zwischen den Wellenbergen ist die Wellenlänge, nochmals an der Skizze rechts unten verdeutlicht. Die roten Pfeile sind die Wellennormalen oder auch Wellenstrahlen. Sie sind Richtungspfeile und stehen immer senkrecht auf den Wellenfronten. Betrachtet man einen kleinen Teil einer sehr großen Kreiswelle, kann dieser annähernd durch horizontale Wellenfronten dargestellt werden, wie oben rechts geschehen.
Huygens hat sich nun überlegt, wie die Ausbreitung einer Welle zustande kommt. Er nahm an, daß jeder Punkt einer Wellenfront, Ausgangspunkt neuen Elementarwellen ist. Diese Elementarwellen überlagern sich. Die Einhüllende aller Elementarwellen, ergibt dann eine neue Wellenfront. Die folgende Skizze soll das erläutern:
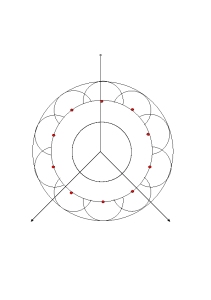
Das Huygens’sche Prinzip.
Die roten Punkte auf der Wellenfront sind Ausgangspunkte neuer Elementarwellen, hier als Teilkreise dargestellt. Die Elementarwellen überlagern sich, die Einhüllende bildet die neue Wellenfront. Dort entstehen wieder neue Elementarwellen, und so setzt sich die Ausbreitung der Welle fort. Die Welle kann sich in alle Richtungen ausbreiten. Die skizzierten Wellenstrahlen stellen daher auch keine bevorzugten Richtungen dar.
Was passiert, wenn nun eine horizontale Wellenfront auf ein Hindernis, wie eine Lochblende fällt? Um das zu versehen, betrachten wir zunächst statt einer engen Lochblende einen engen Spalt, weil die mathematische Beschreibung hier einfacher ist. Physikalisch betrachtet sind die Verhältnisse an Spalt und Lochblende aber identisch.
Betrachten wir eine ebene Wellenfront, die auf einen engen Spalt der Breite l fällt.

Wellenstrahlen die von A und B auf P zulaufen.
Auch hier entstehen, an der den Spalt passierenden Wellenfront, neue Elementarwellen. Zwei Elementarwellen am äußeren Rand, dargestellt durch deren Wellenstrahlen, laufen auf Punkt P zu. Wenn die Spaltbreite l gegenüber der Strecke a sehr klein ist, kann man annehmen, daß beide Wellenstrahlen fast parallel verlaufen. Die Wegstrecke BP ist in diesem Beispiel um die halbe Wellenlänge, also λ/2 länger als die Wegstrecke AP. Das bedeutet, daß die von Punkt B ausgehende Welle etwas später in P ankommt, so daß ein Gangunterschied (Phasenverschiebung) von λ/2 eintritt. Das folgende Bild verdeutlicht nochmals die Phasenverschiebung.
Bei einer Phasenverschiebung von einer halben Wellenlänge, treffen in Punkt P Wellental auf Wellenbauch.

Phasenverschiebung λ /2 . Destruktive Interferenz.
Wenn aber das Wellental einer Welle mit dem Wellenbauch einer anderen Welle aufeinander treffen, (ähnliche Wellenlänge und Orientierung vorausgesetzt), dann löschen sie sich gegenseitig aus. Man nennt das Destruktive Interferenz.
So, nun haben wir alles zusammen, um die Kreise des obigen Beugungsbildes zu erklären. In der folgenden Skizze trifft nochmal eine horizontale Wellenfront mit der Wellenlänge λ auf einen Spalt der Breite d. Auch hier entstehen am Spalt neue Elementarwellen. Die Elementarwellen breiten sich in alle Richtungen aus. 5 Ausgangspunkte von Elementarwellen sind als rote Punkte eingezeichnet. Die Wellenstrahlen breiten sich in Richtung a mit dem Winkel α aus. Alle Wellenstrahlen treffen sich in einem Punkt P, der hier nicht eingezeichnet ist. Wegen der großen Entfernung zum Projektionsschirm im Vergleich zum engen Spalt, können die Wellenstrahlen parallel gezeichnet werden. Das entspricht durchaus der Realität der obigen Aufnahme. Die Lochblende vor dem Laser Pointer hatte einen Durchmesser von ca. 0,15 mm, der Abstand zwischen Lochblende und Projektionsschirm betrug ca. 3000 mm.
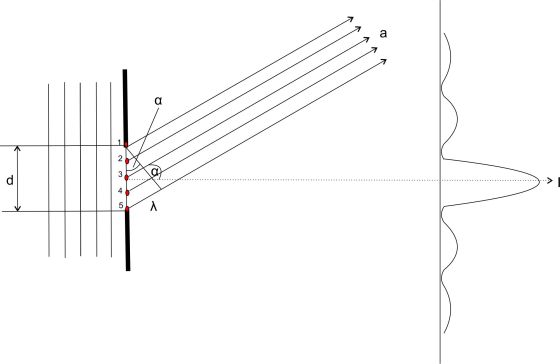
Beugung an einem Einzelspalt mit Darstellung des 1. Minimums.
Betrachtet man einen Einzelspalt genauer, so ist er nicht Ausgangspunkt einer einzelnen Elementarwelle. Vielmehr ist jeder Punkt des Spalts Ausgangspunkt neuer Elementarwellen. Im Bild sind 5 solcher Punkte rot eingezeichnet. Die von ihnen ausgehenden, sich überlagernden Elementarwellen sind durch ihre Wellenstrahlen dargestellt. Sie bewegen sich in Richtung a mit dem Winkel α gegenüber der Horizontalen. Beträgt der Gangunterschied zwischen den beiden äußeren Randstrahlen 1 und 5 gerade λ, so kann man Strahlenpaare finden, deren Gangunterschied gerade λ/2 beträgt. Das sind die Strahlenpaare 1 und 3 sowie 2 und 4 und schließlich 3 und 5. Die Strahlenpaare löschen sich somit alle wegen des Gangunterschieds durch destruktive Interferenz vollständig aus.
Wellenstrahlen die geradlinig verlaufen, bei denen der Winkel α = 0 ist, bilden das Intensitätshauptmaximum, auf dem Bild auf der Mittelachse.
Für das ersten Minimum gilt:
sin α = ± λ/d
Die hier angestellten Überlegungen gelten natürlich auch für Gangunterschiede größer als λ, also für 2λ, 3λ, …
Bei der Beugung an einem Spalt entstehen helle und dunkle Streifen. Für die Minima gilt:
sin αk = k·λ/d k = ±1, ± 2, … ( λ Wellenlänge d Spaltbreite)
Zwischen den Minima liegen Nebenmaxima sehr geringer Intensität. Die Bedingung für die Nebenmaxima lautet:
sin αk = (2k + 1)·λ/2d k= ±1, ±2, …
Es besteht physikalisch kein Unterschied zwischen der Beugung an einem Spalt oder an einer runden Öffnung, wie einer Lochblende mit dem Radius r. Aber die mathematische Beschreibung ist erheblich schwieriger. Bei Lochblenden entstehen dann nicht Beugungsstreifen wie am Spalt sondern Beugungskreise, wie sie auf dem obigen Foto zu sehen sind.
Unser Ausgangspunkt war das Schließen der Aperturblende am Mikroskop. Je weiter man sie schließt, umso stärker treten Beugungserscheinungen auf, die das mikroskopische Bild negativ beeinträchtigen. Beugung von Lichtwellen tritt immer auf, wenn diese auf Hindernisse treffen. Ein Blendenrand oder die Fassung eines Objektivs sind solche Hindernisse. Je kleinen ein Öffnung ist, umso stärker treten Beugungserscheinungen hervor. Ohne die kleine Aluminiumlochblende vor dem Laser Pointer hätten wir auf dem obigen Foto einen kleinen roten Punkt gesehen, wie wir es von einem Laser Pointer gewöhnt sind. Das Hindernis Lochblende mit einem Durchmesser von ca. 0,15 mm hat die Beugungserscheinungen aber voll zu Tage treten lassen.
So liebe Freunde der Mikrokristalle, es ist Spargelzeit. Da habe ich nochmal zur Asparaginsäure gegriffen, die, wie der Name schon sagt, Bestandteil dieses feinen Gemüses ist. Ich habe ca. 250 mg in 10 ml Isopropanol/dest. Wasser 1:1 heiß gelöst und einen Tropfen auf einen Objektträger gegeben. Die Kristallisation setzt meist schon nach wenigen Minuten ein. (Manchmal benötigt man aber etwas Geduld).
Hier die Ergebnisse:

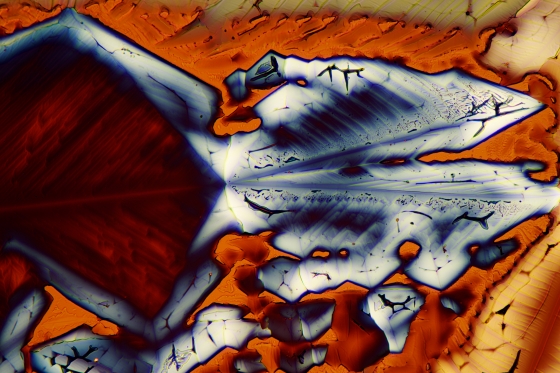
Asparaginsäure fotografiert im polarisierten Licht. Vergrößerung 100x.

Asparaginsäure fotografiert im polarisierten Licht. Vergrößerung 100x.
Bei dem unteren Foto könnte man meinen, ein reißende Fluss bewegt sich durch eine Berglandschaft.
Man kann sich fragen, ob der Aufwand gerechtfertigt war, um das Phänomen der Beugung so detailliert zu beschreiben. Aber mit den Erkenntnissen die wir aus dem Beugungsexperiment gewonnen haben, können wir ohne weiteren Aufwand berechnen, wo die Grenze des Auflösungsvermögens bei optischen Mikroskopen liegt, mit anderen Worten, welche maximale Vergrößerung überhaupt möglich ist. Und das ist doch eine wirklich interessante Frage.
Das liebe Freunde der Mikrokristalle, wird daher auch das Thema meines nächsten Blogbeitrags sein.
Bis dahin wünsche ich eine gute Zeit.
H-D-S